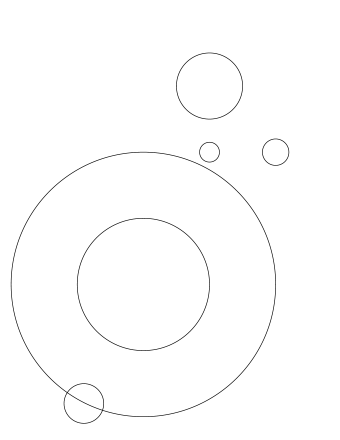
A number of circles are given. A circle may be disjoint from other circles, overlapping with some other circles, or even totally surrounding or surrounded by another circle.
 |
 |
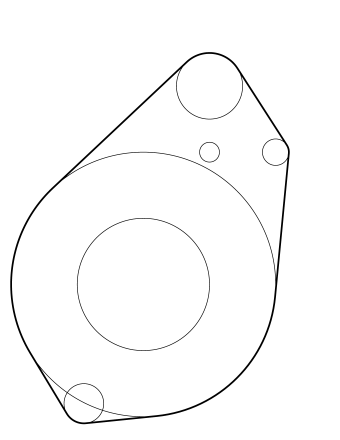
| Figure 1. given circles | Figure 2. rope layout |
We want to enclose all these circles by a rope. Of course, the length of the rope should be minimized. For example, given circles of Figure 1, the rope should run as shown in Figure 2.
Your job is to write a program which finds the rope layout, and computes the minimum length of the rope. The thickness of the rope is negligible.
The input consists of multiple data sets. Each data set is given in the following format.
n x1 y1 r1 x2 y2 r2 ... xn yn rn
The first line of a data set contains an integer n, which is the number of circles. n is positive, and does not exceed 100.
The following n lines are descriptions of circles. Three values in a line are x-coordinate and y-coordinate of the center, and radius (called r in the rest of the problem) of the circle, in this order. Each value is given by a decimal fraction, with 3 digits after the decimal point. Values are separated by a space character.
Each of x, y and r is never less than 0.01, and is never greater than 100.0. Two circles are never the same. Speaking more precisely, at least one of x, y or r of two circles has a difference larger than 0.01.
The end of the input is indicated by a line containing a zero.
For each data set, the minimum length of the rope should be printed, each in a separate line. The printed values should have 5 digits after the decimal point. They may not have an error greater than 0.00001.
1 10.000 10.000 10.000 4 10.000 10.000 5.000 30.000 10.000 5.000 30.000 30.000 5.000 10.000 30.000 5.000 6 10.000 20.000 10.000 20.000 50.000 5.000 30.000 40.000 2.000 1.000 2.000 3.000 10.000 20.000 20.000 20.000 40.000 1.500 0
62.83185 111.41593 153.16052
Test your program against this first input data.